Supermoon Eclipse 2015

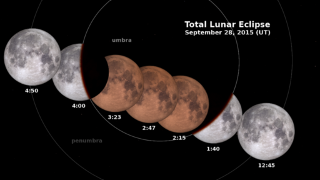
On September 28, 2015 (the night of the 27th in many places), the Moon will be full at the same time that it is closest to Earth for the year, a coincidence sometimes called a supermoon. As it happens, this largest Full Moon occurs within the Earth's shadow, creating the added spectacle of a total lunar eclipse.

The Moon's orbit is very slightly elliptical and therefore somewhat off-center relative to the Earth. Each month, the Moon passes through points in its orbit called perigee and apogee, the closest and farthest points from the Earth for that month. Some perigees are a little closer than others. The closest perigee for 2015 occurs on September 28 at around 1:52 Universal Time, when the Moon will be 356,877 kilometers (221,753 miles) away. This is only an hour before the time of peak full Moon at 2:51 UT, when the Moon's ecliptic longitude differs from the Sun's by exactly 180 degrees.

All of this takes place during a total lunar eclipse. The Moon makes first contact with the umbra, the central part of the Earth's shadow, at 1:07 UT, and it doesn't completely emerge until 4:27 UT.

If we define a supermoon as a Full Moon that coincides with the closest perigee in a given year, then supermoons occur every 14 months, with occasional skips. The anomalistic month — the time between two perigees — is two days shorter than the cycle of phases, called the synodic month; the perigees "lap" the phases after 14 months.

Total lunar eclipses involve a third cycle, the draconic month. The Moon's tilted orbit crosses the Earth-Sun plane at one of two points called nodes; a draconic month is the time it takes the Moon to return to the same node. Total lunar eclipses happen when a node crossing coincides with a Full Moon. Only then does the Moon's orbit carry it close enough to the Earth-Sun line to actually pass through the shadow cast by the Earth.

A supermoon eclipse requires the alignment of all three cycles, the synodic, anomalistic, and draconic months, and this happens every 18 years 11 days, a period known as a saros. Eclipses separated by this period tend to share certain properties and are grouped into families, or saros series. The 2015 supermoon eclipse is the first in Saros 137. There will be seven more supermoon eclipses in this series, the last in December of 2141.

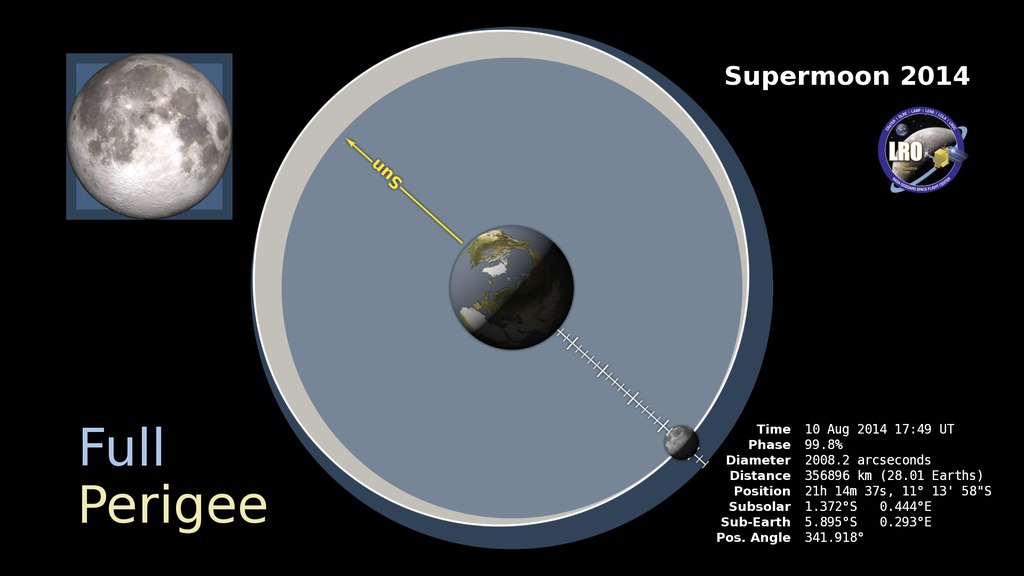
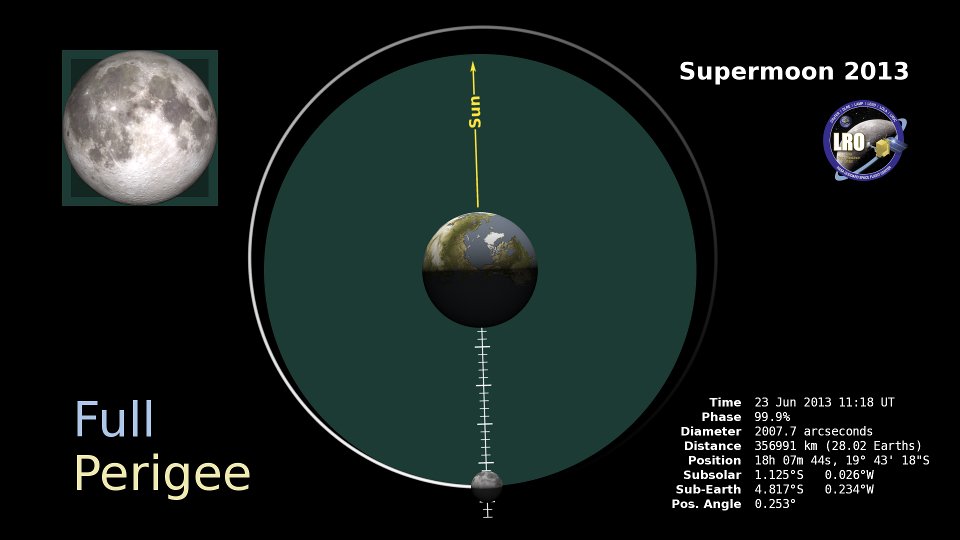
The animation begins at the end of August showing that perigee and Full Moon miss each other by about a day. It then shows apogee on September 14, when the Moon is almost 32 Earth diameters away. It ends on September 28, the day of the supermoon eclipse, when the distance to the Moon is 28 Earth diameters. The Moon graphic in the upper left shows the change in the Moon's apparent size as it moves closer and farther in its orbit, as well as its copper color during the eclipse.

The relative sizes of the Earth and Moon in the main orbit graphic are exaggerated by a factor of 15 to make them more easily visible.

Eccentricity

r_a / r_p = 1.139

e = 1 − 2 / (( r_a / r_p ) + 1 )

There are two major cycles apparent in the graph, one with a period of roughly a month (31.8 days) and the other repeating about every half-year (205.9 days). Both of these cycles arise from the orientation of the Moon's orbit with respect to the Sun.

The graph is based on an expression for the varying or osculating eccentricity in (Simon et al. 1994). Note that the calculation we did earlier, using the closest perigee and the farthest apogee, isn't physically valid, since these occur at two different points in time.

See 2015 Lunar Eclipse Gallery