Plasma Zoo: Particle Drift in a Magnetic Gradient

Motions of charged particles in electromagnetic fields are important in understanding the behaviors of plasmas in space. In Plasma Zoo, we present visualizations of particle motions in simple electromagnetic field configurations.

One of the more fundamental motions of charged particles in a magnetic field is gyro-motion, or cyclotron motion. If a charged particle is moving in a magnetic field, the particle experiences a force perpendicular to the direction of the charge motion and the field. This direction is determined by the Right-Hand Rule (Wikipedia). The resulting force directs the motion in a curve such that if we view along the direction the magnetic field is pointing, we will see the positive particles gyrate anti-clockwise while the negative particles gyrate clockwise.

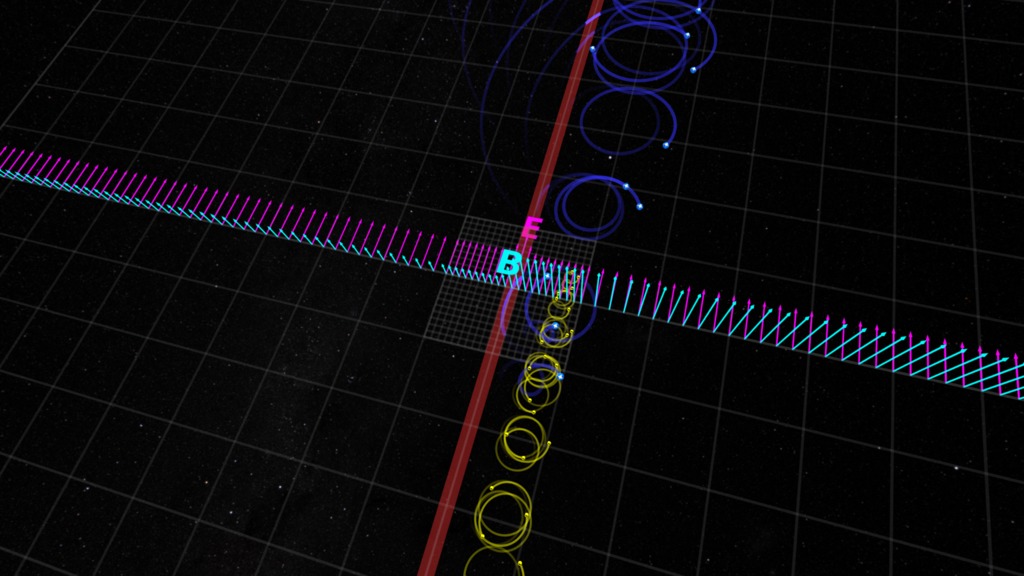
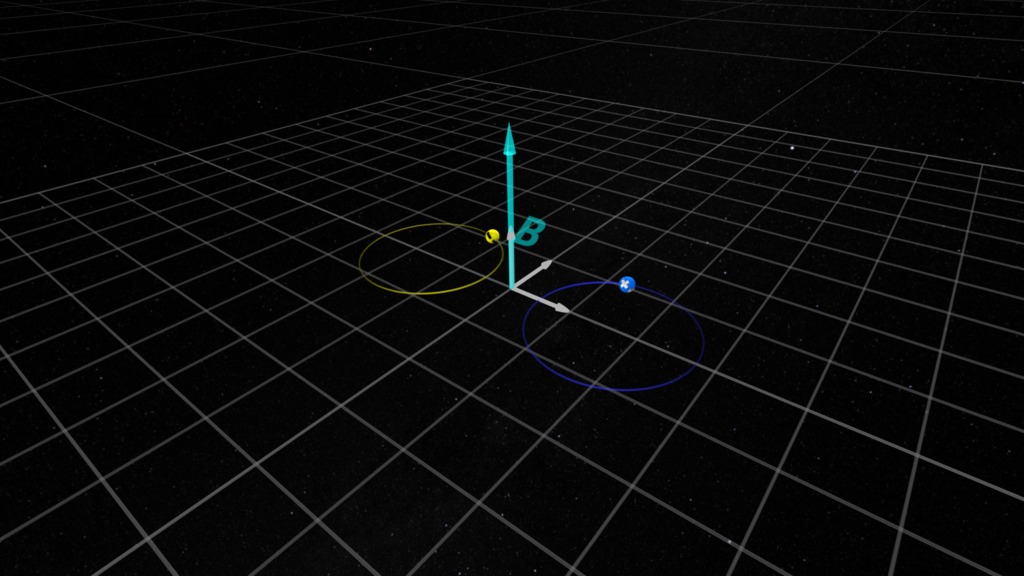
Consider a magnetic field which fills a region of space with uniform intensity and direction. Here we represent that magnetic field (designated with the letter 'B') as a cyan (light green) arrow, its direction representing the direction of the field vector. In examples Plasma Zoo: Gyromotion in Two Dimensions and Plasma Zoo: Gyromotion in Three Dimensions, we looked at cases where the magnetic field has a constant magnitude and direction through the region of space. But what happens if the magnetic field intensity varies in the region where the particles are moving? Such changes in intensity with position are called gradients. When a road is sloping, such as on a hillside, we describe the angle of the slope as the grade of the road, which is a term derived from the similar concept.

In this example, the magnetic field is constant in one direction, but is stronger further away from the observer (represented by the longer cyan arrow) and weaker closer to the observer (represented by the shorter cyan arrow).

So what happens with the particle motion?

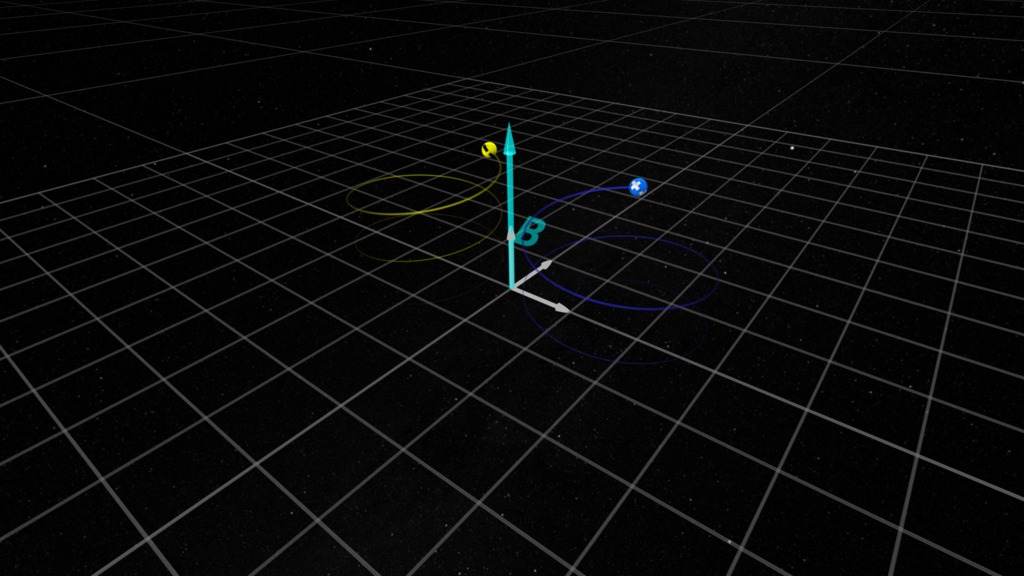
In regions where the magnetic field is stronger the gyro-radius is smaller - the particle wants to move in a tighter circle. In regions where the field is weaker, the gyro-radius is larger - the particle wants to move in a wider circle.

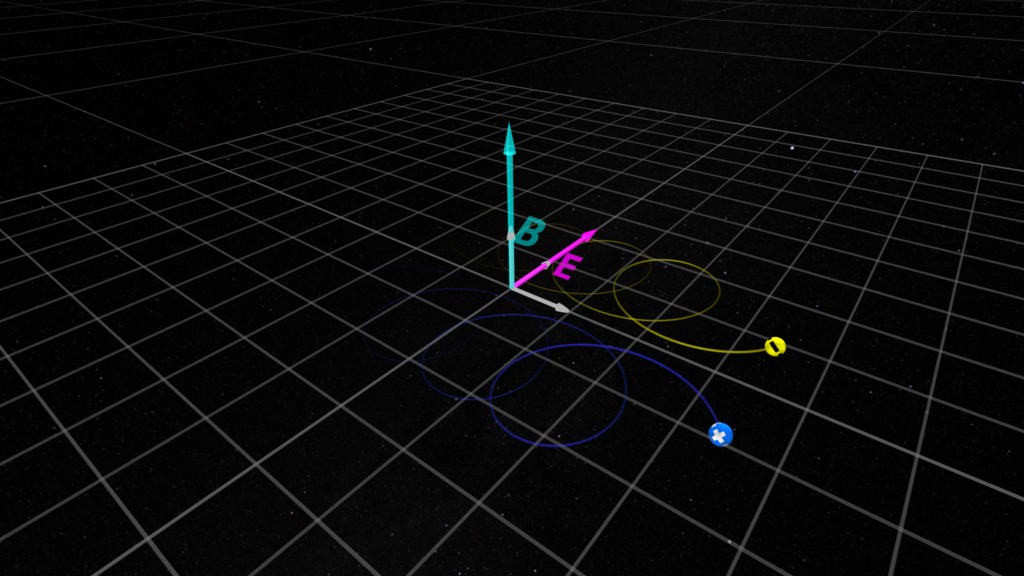
The net effect of the gyro-radius changing as the particle moves is these differing gyro-radii add up to make the particle slowly drift in one direction. Note that the particles drift in opposite directions depending on their electric charge is positive ('+') or negative ('-').

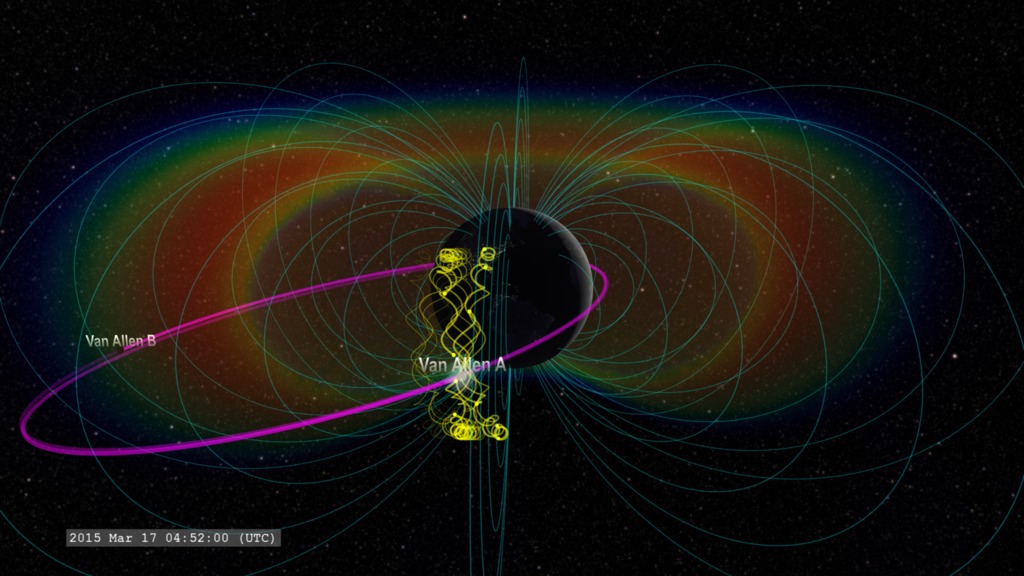
While the positive charge is moving away from the observer, and a negative charge is moving towards the observer, these two motions contribute to a net positive charge away from the observer. This motion in a magnetic gradient drives the ring current (Wikipedia) in Earth's magnetosphere.

Important Note: The example here shows particles with the same speed and mass. If the masses are different (for example, a positive proton has about 1836 times more mass than an electron), the radius of the gyromotion will be proportionally larger for the same speed.